Research
Our research is inherently interdisciplinary, and touches a wide variety of topics: from biomolecular physics, to math, to computational science. Most of our work is related to the solution of the Poisson-Boltzmann equation using boundary integral methods, and applications of this in biophysics.
This research has been funded by ANID, through their FONDECYT and FONDEF programs, and USM, by means of internal funding from the DGIIE (Office of Research, Innovation and Entrepreneurship). Their support is highly appreciated.
For an up-to-date list of publications, visit Christopher’s google scholar profile
The Poisson-Boltzmann equation for molecular electrostatics
Our main research line is in the development of computer codes to simulate protein solvation with continuum electrostatic models (ie. considering the solvent as a dielectric region). This yields system of PDEs where the Poisson and Poisson-Boltzmann equations are coupled on the molecular surface, which we represent with boundary integral equations. We solve this numerically using boundary element methods, accelerated with fast methods that run on GPUs. Most of our work has been implemented on two codes:
- PyGBe, an in-house BEM code that runs of GPUs.
- PBJ (Poisson-Boltzmann & Jupyter), a Jupyter notebook based codethat uses the Bempp library.
Some applications we’ve explored with our codes are
- Protein-surface interaction
- Viral disassembly
- Nonpolar solvation
- LSPR biosensor sensitivity
- Polarizable force fields
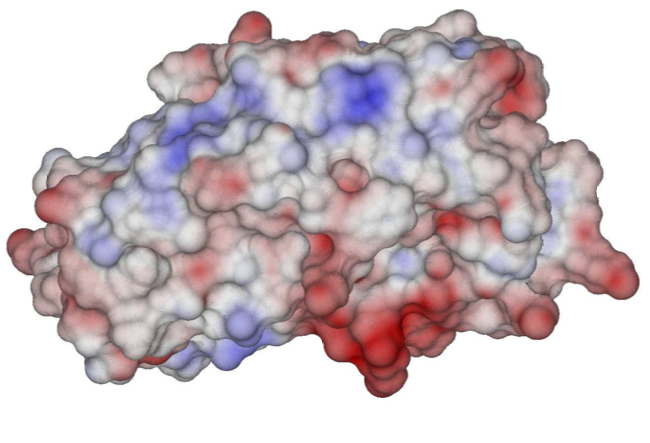

Left: Electrostatic potential on the molecular surface of a HIV-1 protease-substrate complex. Right: BEM mesh for lysozyme.
Fast and accurate computations
One of the main disadvantages of BEM is that it generates dense matrices, yielding a O(N^2) scaling in memory and computer time that limits its applicability. Because of this, we’re very interested in developing algorithms that improve this scaling to O(NlogN) or even O(N). More specifically, I’ve mostly worked with the treecode algorithm, which accelerates N-body problems to O(NlogN) by approximating far-away interactions to centers of expansion.
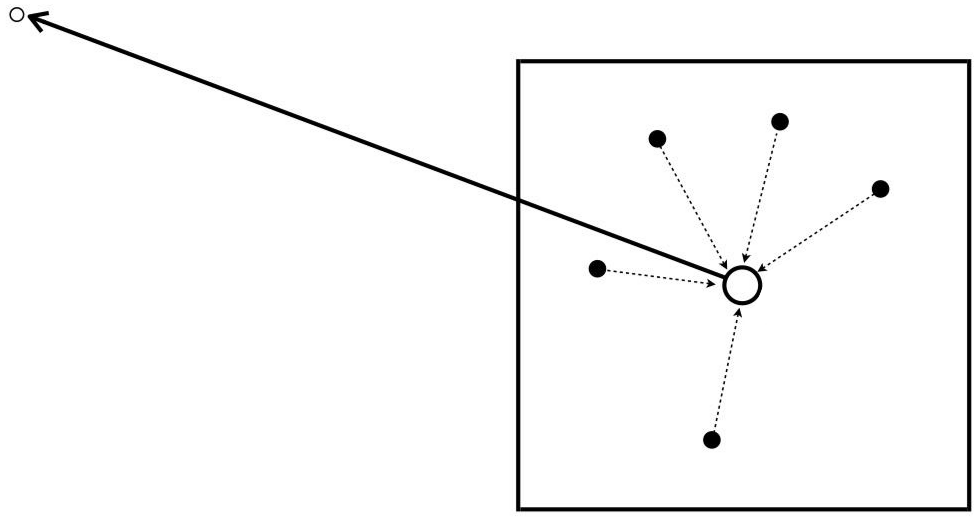
Sketch of the treecode far-field approximation. White dots are ‘targets’ and black dots ‘sources’ of mass.
To develop the most efficient code possible, we have also explored alternative boundary integral formulations, preconditioners, and adaptive mesh refinement.
High performance computing
Many real-life applications are just too big to model on a single CPU, and we require parallel processing and modern hardware to tackle them in reasonable time. Most of my work has been based in the use of GPUs for numerical algorithms, and we’ve been exploring to extend those algorithms to use multiple CPUs and GPUs.
